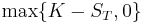Put option

A put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity. One party, the buyer of the put, has the right, but not an obligation, to sell the asset at the strike price by the future date, while the other party, the seller, has the obligation to buy the asset at the strike price if the buyer exercises the option.

If the strike is K and maturity time is T, if the buyer exercises the put at a time t, the buyer can expect to receive a payout of K-S(t), if the price of the underlying S(t) at that time is less than K. The exercise t must occur by time T; precisely what exact times are allowed is specified by the type of put option. An American option can be exercised at any time before or equal to T; a European option can be exercised only at time T; a Bermudan option can be exercised only on specific dates listed in the terms of the contract. If the option is not exercised by maturity, it expires worthless. (Note that the buyer will not exercise the option at an allowable date if the price of the underlying is greater than K.)

The most obvious use of a put is as a type of insurance. In the protective put strategy, the investor buys enough puts to cover their holdings of the underlying so that if a drastic downward movement of the underlying's price occurs, they have the option to sell the holdings at the strike price. Another use is for speculation: an investor can take a short position in the underlying without trading in it directly.

Puts may also be combined with other derivatives as part of more complex investment strategies, and in particular, may be useful for hedging. Note that by put-call parity, a European put can be replaced by buying the appropriate call option and selling an appropriate forward contract.

Contents

Instrument models

The terms for exercising the option's right to sell it differ depending on option style. A European put option allows the holder to exercise the put option for a short period of time right before expiration, while an American put option allows exercise at any time before expiration.

The most widely-traded put options are on equities, but they are traded on many other instruments such as interest rates (see interest rate floor) or commodities.

The put buyer either believes that the underlying asset's price will fall by the exercise date or hopes to protect a long position in it. The advantage of buying a put over short selling the asset is that the option owner's risk of loss is limited to the premium paid for it, whereas the asset short seller's risk of loss is unlimited (its price can rise greatly, in fact, in theory it can rise infinitely, and such a rise is the short seller's loss). The put buyer's prospect (risk) of gain is limited to the option's strike price less the underlying's spot price and the premium/fee paid for it.

The put writer believes that the underlying security's price will rise, not fall. The writer sells the put to collect the premium. The put writer's total potential loss is limited to the put's strike price less the spot and premium already received. Puts can be used also to limit the writer's portfolio risk and may be part of an option spread.

The put buyer is short on the underlying asset of the put, but long on the put option itself. That is, the buyer wants the value of the put option to increase by a decline in the price of the underlying asset below the strike price. The writer (seller) of a put is long on the underlying asset and short on the put option itself. That is, the seller wants the option to become worthless by an increase in the price of the underlying asset above the strike price. Generally, a put option that is purchased is referred to as a long put and a put option that is sold is referred to as a short put.

A naked put, also called an uncovered put, is a put option whose writer (the seller) does not have a position in the underlying stock or other instrument. This strategy is best used by investors who want to accumulate a position in the underlying stock, but only if the price is low enough. If the buyer fails to exercise the options, then the writer keeps the option premium as a "gift" for playing the game.

If the underlying stock's market price is below the option's strike price when expiration arrives, the option owner (buyer) can exercise the put option, forcing the writer to buy the underlying stock at the strike price. That allows the exerciser (buyer) to profit from the difference between the stock's market price and the option's strike price. But if the stock's market price is above the option's strike price at the end of expiration day, the option expires worthless, and the owner's loss is limited to the premium (fee) paid for it (the writer's profit).

The seller's potential loss on a naked put can be substantial. If the stock falls all the way to zero (bankruptcy), his loss is equal to the strike price (at which he must buy the stock to cover the option) minus the premium received. The potential upside is the premium received when selling the option: if the stock price is above the strike price at expiration, the option seller keeps the premium, and the option expires worthless. During the option's lifetime, if the stock moves lower, the option's premium may increase (depending on how far the stock falls and how much time passes). If it does, it becomes more costly to close the position (repurchase the put, sold earlier), resulting in a loss. If the stock price completely collapses before the put position is closed, the put writer potentially can face catastrophic loss. In order to protect the put buyer from default, the put writer is required to post margin. The put buyer does not need to post margin because the buyer would not exercise the option if it had a negative payoff.

Example of a put option on a stock

Buying a put

A Buyer thinks the price of a stock will decrease. He pays a premium which he will never get back, unless it is sold before it expires. The buyer has the right to sell the stock at the strike price.

Writing a put

The writer receives a premium from the buyer. If the buyer exercises his option, the writer will buy the stock at the strike price. If the buyer does not exercise his option, the writer's profit is the premium.

Trader A's total earnings (S) can be calculated at $500. The sale of the 100 shares of stock at a strike price of $50 to Trader B = $5,000 (P). The purchase of 100 shares of stock at $40 = $4,000 (Q). The put option premium paid to trader B for buying the contract of 100 shares at $5 per share, excluding commissions = $500 (R). Thus S = P - (Q+R) = $5,000 - ($4,000+$500) = $500.

A put option is said to have intrinsic value when the underlying instrument has a spot price (S) below the option's strike price (K). Upon exercise, a put option is valued at K-S if it is "in-the-money", otherwise its value is zero. Prior to exercise, an option has time value apart from its intrinsic value. The following factors reduce the time value of a put option: shortening of the time to expire, decrease in the volatility of the underlying, and increase of interest rates. Option pricing is a central problem of financial mathematics.

Payoff of a put

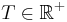These examples lead to the following formal reasoning. Fix \mathcal{O} an underlying financial instrument. Let \Pi be a put option for this instrument, purchased at time 0, expiring at time T\in\mathbb{R}^{%2B}, with exercise (strike) price of 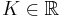K\in\mathbb{R}; and let S:[0,T]\to\mathbb{R} be the price of the underlying instrument.

Assume the owner of the option 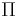\Pi, wants to not take a loss, and does not want to actually possess the underlying instrument, \mathcal{O}. Then either (i) the person will purchase \mathcal{O} at expiry, and then immediately exercise the selling option; or (ii) the person will not exercise the option (which subsequently becomes worthless).

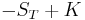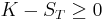In (i), the pay-off would be -S_{T}%2BK; in (ii) the pay-off would be 0. So if K-S_{T}\geq 0 (i) or (ii) occurs; if 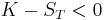K-S_{T}<0 then (ii) occurs.

Hence the pay-off, i.e. the value of the put option at expiry, is

\operatorname{max}\{K-S_{T},0\}

 

 

 

 

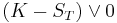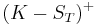which is alternatively written (K-S_{T})\vee 0 or (K-S_{T})^{%2B}.

See also

Options

External links

Options
Terms
Swaps
Forwards and Futures
Other derivatives
Market issues